Time dilation
Gravitational time dilation is a physics concept about changes in the passage of time, caused by general relativity. A clock in outer space moves quicker than a clock on Earth. Heavy things like planets create a gravitational field that slows down time nearby. An example of gravity causing time dilation is that if an object is near a black hole its time will slow relative to that of time on earth. This means that a clock on a spaceship far away from any planet would move faster than a clock near Earth.
This is different from time dilation explained by special relativity, which says fast objects move more slowly through time. Close satellites like the International Space Station move very quickly to orbit the Earth, so they are slowed down. Because the ISS is in low Earth orbit (LEO), time dilation due to gravity is not as strong as time dilation due to its speed, so a clock on it is slowed down more than it is sped up. An object in Geostationary orbit moves less quickly and is farther away from Earth, so gravitational time dilation is stronger, and clocks move quicker than in LEO. This means that engineers need to pick different clocks for different orbits. GPS satellites work because they know about both kinds of time dilation.[1]
Case #1: In special relativity, clocks that are moving run slower, according to a stationary observer's clock. This effect does not come from workings of the clocks, but from the nature of spacetime.
Case #2: the observers may be in positions with different gravitational masses. In general relativity, clocks that are near a strong gravitational field run slower than clocks in a weaker gravitational field.
If you were to have a rotor, or motor, moving at a very fast speed (any measurement of speed will cause time dilation just in varying amounts) and have a beam of sorts with a capsule, the faster it spins the more time changes.
This could theoretically make a time machine although it could only go forward and would be very dangerous.
Evidence
Experiments support both aspects of time dilation.[2][3][4][5]
Time dilation due to relative velocity
The formula for determining time dilation in special relativity is:
- [math]\displaystyle{ \Delta t' = \frac{\Delta t}{\sqrt{1-v^2/c^2}} \, }[/math]
where
- [math]\displaystyle{ \Delta t \, }[/math] is the time interval for an observer (e.g. ticks on his clock) – this is known as the proper time,
- [math]\displaystyle{ \Delta t' \, }[/math] is the time interval for the person moving with velocity v with respect to the observer,
- [math]\displaystyle{ v \, }[/math] is the relative velocity between the observer and the moving clock,
- [math]\displaystyle{ c \, }[/math] is the speed of light.
It could also be written as:
- [math]\displaystyle{ \Delta t' = \gamma \Delta t \, }[/math]
where
- [math]\displaystyle{ \gamma = \frac{1}{\sqrt{1-v^2/c^2}} \, }[/math] is the Lorentz factor.
A simple summary is that more time is measured on the clock at rest than the moving clock, therefore, the moving clock is "running slow".
When both clocks are not moving, relative to each other, the two times measured are the same. This can be proven mathematically by
- [math]\displaystyle{ \Delta t' = \frac{\Delta t}{\sqrt{1-0/c^2}} = {\Delta t} \, }[/math]
For example: In a spaceship moving at 99% of the speed of light, a year passes. How much time will pass on earth?
- [math]\displaystyle{ v=0.99c \, }[/math]
- [math]\displaystyle{ \Delta t=1\, }[/math] year
- [math]\displaystyle{ \Delta t'=? \, }[/math]
Substituting into :[math]\displaystyle{ \Delta t' = \frac{\Delta t}{\sqrt{1-v^2/c^2}} \, }[/math]
- [math]\displaystyle{ \Delta t'=\frac{1}{\sqrt{1-(.99c)^{2}/c^{2}}}=\frac{1}{\sqrt{1-\frac{(.99)^{2}(c)^{2}}{c^{2}}}}=\frac{1}{\sqrt{1-(.99)^{2}}} }[/math]
- [math]\displaystyle{ =\frac{1}{\sqrt{1-0.9801}}=\frac{1}{\sqrt{0.0199}}=7.08881205 }[/math]years
So approximately 7.09 years will pass on earth, for each year in the spaceship.
In ordinary life today, time dilation had not been a factor, where people move at speeds much less than the speed of light, the speeds are not great enough to produce any detectable time dilation effects. Such vanishingly small effects can be safely ignored. It is only when an object approaches speeds on the order of 30,000 kilometres per second (67,000,000 mph) (10% the speed of light) that time dilation becomes important.
However, there are practical uses of time dilation. A big example is with keeping the clocks on GPS satellites accurate. Without accounting for time dilation, the GPS result would be useless, because time runs faster on satellites so far from Earth's gravity. GPS devices would calculate the wrong position due to the time difference if the space clocks were not set to run slower on Earth to offset the quicker time in high Earth orbit (geostationary orbit).
Time Dilation Media
Left: Observer at rest measures time 2L/c between co-local events of light signal generation at A and arrival at A.Right: Events according to an observer moving to the left of the setup: bottom mirror A when signal is generated at time t'=0, top mirror B when signal gets reflected at time t'=D/c, bottom mirror A when signal returns at time t'=2D/c
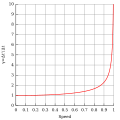
Lorentz factor as a function of speed (in natural units where c = 1). Notice that for small speeds (as v tends to zero), γ is approximately 1.
Daily time dilation over circular orbit height split into its components. On this chart, only Gravity Probe A was launched specifically to test general relativity. The other spacecraft on this chart (except for the ISS, whose range of points is marked "theory") carry atomic clocks whose proper operation depend on the validity of general relativity.
References
- ↑ Ashby, Neil (2003). "Relativity in the Global Positioning System". Living Reviews in Relativity. 6 (1) 1: 16. Bibcode:2003LRR.....6....1A. doi:10.12942/lrr-2003-1. PMC 5253894. PMID 28163638.
- ↑ Blaszczak Z. 2007 (15 April 2010). Laser 2006. Springer. p. 59. ISBN 978-3540711131.
- ↑
Hasselkamp D; Mondry E. & Scharmann A. 1979 (1979). "Direct observation of the transversal Doppler-shift". Zeitschrift für Physik A. 289 (2): 151–155. Bibcode:1979ZPhyA.289..151H. doi:10.1007/BF01435932. S2CID 120963034.
{{cite journal}}: CS1 maint: multiple names: authors list (link) - ↑ Chou C.W. et al 2010 (2010). "Optical clocks and relativity". Science. 329 (5999): 1630–1633. Bibcode:2010Sci...329.1630C. doi:10.1126/science.1192720. PMID 20929843. S2CID 206527813.
- ↑ Pound R.V. & Snider J.L. 1964 (1964). "Effect of gravity on nuclear resonance". Physical Review Letters. 13 (18): 539–540. Bibcode:1964PhRvL..13..539P. doi:10.1103/PhysRevLett.13.539.