Cheletropic reaction

Figure 1. Pericyclic Reactions

A cheletropic reaction is a type of pericyclic reaction where one atom on one of the reagents gets two new bonds. A pericyclic reaction is one that involves a transition state with a cyclic array of atoms and an associated cyclic array of interacting orbitals. A reorganization of σ and π bonds occurs in this cyclic array.

Cheletropic reactions are a subclass of cycloadditions. What sets cheletropic reactions apart is that on one of the reagents, both new bonds are being made to the same atom. A few examples are shown to the right in Figure 1. In the first case, the single atom is the carbon atom in the carbonyl group. That carbon atom ends up in carbon monoxide. The end result is making two new bonds to one atom. The first two examples are known as "cheletropic extrusions" because a small stable molecule is given off in the reaction. The driving force for these reactions is often the entropic benefit of releasing a gas (e.g. CO or N₂).

Theoretical analysis

Because of the geometry of the molecules involved in cheletropic reactions, they confirm a number of predictions made by theoretical chemists. Cheletropic reactions confirm the conservation of molecular orbital symmetry.

In the pericyclic transition state, a small molecule donates two electrons to the ring. Two possible geometries can explain the reaction. The small molecule can approach in either a linear or non-linear way. In the linear approach, the electrons in the orbital of the small molecule are pointed directly at the π system of the big molecule. In the non-linear approach, the orbital approaches at a slightly off angle. The π-systems ability to rotate as the small molecule approaches is crucial in forming new bonds. The direction of rotation will be different depending on how many π-electrons are in the system. A diagram of a two-electron fragment approaching a four-electron π-system using frontier molecular orbitals is shown below. The rotation will be disrotatory if the small molecule approaches linearly and conrotatory if the molecule approaches non-linearly. Disrotatory and conrotatory tell how the bonds in the π-system are rotating. Disrotatory means opposite directions while conrotatory means the same direction. This is also shown in the diagram below.

Using Huckel's Rule, one can tell if the π-system is aromatic or anti-aromatic. If aromatic, linear approaches use disrotatory motion while non-linear approaches use conrotatory motion. The opposite goes with an anti-aromatic system. Linear approaches will have conrotatory motion while non-linear approaches will have disrotatory motion.

Thermodynamics

When sulfur dioxide reacts with butadiene and isoprene, two different products result. The reaction mechanism will control what gets made. A kinetic product and a thermodynamic product are both possible. More of the thermodynamic product gets made than the kinetic product. The kinetic product comes from a Diels–Alder reaction, while a cheletropic reaction makes a more thermodynamically stable product. The cheletropic pathway is used more because it makes to a more stable five-membered ring adduct. The scheme below shows the difference between the two products. The path to the left shows the thermodynamic product, while the path to the right shows the kinetic product. Suarez and Sordo showed this in 1995. They showed this both with experiments and using Gaussian calculations.

Kinetics

One example of this is the cheletropic reactions of 1,3-dienes with sulfur dioxide. Chemists have carefully looked at the kinetics of this reaction. In 1976, Isaacs and Laila measured the kenetic factors for the addition of sulfur dioxide to butadiene derivatives. Rates of addition were monitored in benzene at 30 °C with an initial twentyfold excess of diene. They used a spectrophotometer to study light at 320 nm to measure the disappearance of SO₂. The reaction showed "pseudo first-order kinetics". The chemists found that electron-withdrawing groups on the diene decreased the rate of reaction. Also, the reaction rate was affected considerably by steric effects of 2-substituents, with more bulky groups increasing the rate of reaction. (In other words, the larger the group of atoms hanging from the second carbon atom, the quicker the reaction ran.) The authors attribute this to the tendency of bulky groups to favor the cisoid conformation of the diene which is essential to the reaction (see table below). In addition, the rates at four temperatures were measured for seven of the dienes. From these measurements, chemists used the Arrhenius equation to calculate the enthalpy of activation (ΔH^‡) and entropy of activation (ΔS^‡) for each reaction. This was one of the first important efforts to study the kenetics of a cheletropic reaction.

-Butadiene	104 k /min−1 (30 °C) (± 1-2%) absolute	104 k /min−1 (30 °C) (± 1-2%) relative	ΔH‡ /kcal mol−1	ΔS‡ /cal mol−1 K−1
2-methyl	1.83	1.00	14.9	-15
2-ethyl	4.76	2.60	10.6	-20
2-isopropyl	13.0	7.38	12.5	-17
2-tert-butyl	38.2	20.8	10.0	-19
2-neopentyl	17.2	9.4	11.6	-18
2-cloro	0.24	0.13	N/A	N/A
2-bromoethyl	0.72	0.39	N/A	N/A
2-p-tolyl	24.7	13.5	10.4	-19
2-phenyl	17.3	9.45	N/A	N/A
2-(p-bromophenyl)	9.07	4.96	N/A	N/A
2,3-dimethyl	3.54	1.93	12.3	-18
cis-1-methyl	0.18	0.10	N/A	N/A
trans-1-methyl	0.69	0.38	N/A	N/A
1,2-dimethylene-cyclohexane	24.7	13.5	11.4	-16
2-methyl-1,1,4,4-d4	1.96	N/A	N/A	N/A

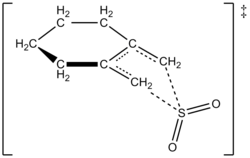
Monnat, Vogel, and Sordo, in 2002, measured the kinetics of addition of sulfur dioxide to 1,2-dimethylidenecycloalkanes. They wrote that the reaction of 1,2-dimethylidenecyclohexane with sulfur dioxide can give two different products depending on reaction conditions. The reaction makes the corresponding sultine through a hetero-Diels-Alder reaction under kinetic control (≤ -60 °C), but, under thermodynamic control (≥ -40 °C), the reaction makes the corresponding sulfolene through a cheletropic reaction. The activation enthalpy for the hetero-Diels-Alder reaction is about 2 kcal/mol smaller than that for the corresponding cheletropic reaction. The sulfolene is about 10 kcal/mol more stable than the isometric sultine in CH₂Cl₂/SO₂ solution.

Reaction of 1,2-Dimethylidenecyclohexane with SO₂ Gives a Sultine Through a Hetero-Diels-Alder Reaction Under kinetic Control or a Sulfolene Through a Cheletropic Reaction Under Thermodynamic Control

The authors were able to experimentally work out a rate law at 261.2 K for the reaction of 1,2-dimethylidenecyclohexane with sulfur dioxide to give the corresponding sulfolene. The reaction was first order in 1,2-dimethylidenecyclohexane but second order in sulfur dioxide (see below). This confirmed a prediction of theoretical chemists based on high-level ab initio quantum calculations. Using computational methods, the authors proposed a transition structure for the cheletropic reaction of 1,2-dimethylidenecyclohexane with sulfur dioxide (see figure at right). The reaction is second order in sulfur dioxide because another molecule of sulfur dioxide likely binds to the transition state to help stabilize it. Similar results were found in an 1995 study by Suarez, Sordo, and Sordo which used ab initio calculations to study the kinetic and thermodynamic control of the reaction of sulfur dioxide with 1,3-dienes.

Proposed Transition State for Reaction of 1,2-Dimethylidenecyclohexane with SO₂ to Give a Sulfolene Through a Cheletropic Reaction

[math]\displaystyle{ \frac{d[3]}{dt}=k_2[1][SO_2]^2 }[/math]

Solvent effects

Cheletropic Reaction Studied in Various Solvents

The effect of the solvent of the cheletropic reaction of 3,4-dimethyl-2,5-dihydrothiophen-1,1-dioxide (shown at right) was kinetically investigated in 14 solvents. The reaction rate constants of the forward and reverse reaction in addition to the equilibrium constants were found to be linearly correlated with the E_T(30) solvent polarity scale.

Reactions were done at 120 °C and were studied by 1H-NMR spectroscopy of the reaction mixture. The forward rate k₁ was found to decrease by a factor of 4.5 going from cyclohexane to methanol. The reverse rate k_-1 was found to increase by a factor of 53 going from cyclohexane to methanol, while the equilibrium constant K_eq decreased by a factor of 140. It is suggested that there is a change of the polarity during the activation process as evidenced by relationships between the equilibrium and kinetic data. The authors say that the reaction appears to be influenced by the polarity of the solvent, and this can be shown by the change in the dipole moments when going from reactant to transition state to product. The authors also state that the cheletropic reaction doesn’t seem to be influenced by either solvent acidity or basicity.

The results of this study lead the authors to expect the following behaviors:

1. The change in the solvent polarity will influence the rate less than the equilibrium.

2. The rate constants will be characterized by opposite effect on the polarity: k₁ will slightly decrease with the increase of E_T(30), and k_-1 will increase under the same conditions.

3. The effect on k_-1 will be larger than on k₁.

Carbene Additions to Alkenes

Addition of a Carbene to an Alkene to Form a Cyclopropane

One of the most synthetically important cheletropic reactions is the addition of a singlet carbene to an alkene to make a cyclopropane (see figure at left). A carbene is a neutral molecule containing a divalent carbon with six electrons in its valence shell. Because of this, carbenes are highly reactive electrophiles and generated as reaction intermediates. A singlet carbene contains an empty p orbital and a roughly sp² hybrid orbital that has two electrons. Singlet carbenes add stereospecifically to alkenes, and alkene stereochemistry is retained in the cyclopropane product. The mechanism for addition of a carbene to an alkene is a concerted [2+1] cycloaddition (see figure). Carbenes derived from chloroform or bromoform can be used to add CX₂ to an alkene to give a dihalocyclopropane, while the Simmons-Smith reagent adds CH₂.

Figure 2. A) The Orbitals for Singlet Carbenes B) Non-linear Approach of a) Carbene sp² Orbital and b) Carbene p Orbital

Interaction of the filled carbene orbital with the alkene π system creates a four-electron system and favors a non-linear approach. It is also favorable to mix the carbene empty p orbital with the filled alkene π orbital. Favorable mixing occurs through a non-linear approach (see figure 2 at right). However, while theory clearly favors a non-linear approach, there are no obvious experimental implications for a linear vs. non-linear approach.