Classical mechanics

Classical mechanics is the part of physics that describes how everyday things move and how their motion changes because of forces. If we know how things are moving now, classical mechanics allows us to predict how they will move in the future and how they were moving in the past. We can use classical mechanics to predict how things like planets and rockets move.

Classical mechanics is not accurate when things are the size of atoms or smaller: for those things, we use quantum mechanics instead. Classical mechanics is also not accurate when things move close to the speed of light: for those things, we use special relativity instead.

Position, velocity, and acceleration

Position

The position of an object tells you where it is. For example, if you live in New York City and your friend lives in Seattle, your friend has a position of 3,876 kilometers (2,408 miles) west from you. But your friend would say that you have a position of 3,876 kilometers (2,408 miles) east from them instead. This is because position depends on where "position zero" or the origin is. For you, the origin is in New York City, but for your friend, the origin is in Seattle. So we make sure to always say where the origin is when we talk about position.

We talk about position using vectors: we first say a distance (such as 3,000 km) and then the direction (such as east, left, or 38 degrees south). If there is no direction, position is simply distance. Position can sometimes be negative: for example, New York City is 3,876 kilometers (2,408 miles) east of Seattle and Seattle is negative 3,876 kilometers (2,408 miles) east of New York City. However, it is easier to say "west" instead of "negative east".

Velocity

When something moves, its position changes. You may pull a book closer to you, and the book has a new position. Or, you may walk away from your house and you have a new position. The velocity of an object tells you how fast the object changes position, and where it is moving. Velocity is a vector just like position: a car can move "160 kilometers per hour west" (100 miles per hour west) or "31 miles per hour south" (50 kilometers per hour south). Since position can be negative, velocity can be negative too.

Acceleration

When something speeds up or slows down, its velocity changes. The acceleration of an object tells you how fast the object speeds up or slows down. Acceleration is a vector, too, and we can use negative acceleration when we want to say that an object slows down: for example, if you drive your car south and slow down, your acceleration is positive going north but negative going south.

Newton's three laws

A page from Newton's book about the three laws of motion

Newton's laws of motion are important to classical mechanics. Isaac Newton discovered them. They tell us how forces change how things move, but they do not say what causes the forces.

Newton's first law

Newton's first law of motion says that objects do not change how they move unless something pushes or pulls them. Things that push or pull objects are called forces.

Before Isaac Newton, people thought that things do not move forever: they will always stop even if nothing touches them. On Earth, this seems correct: if you roll a ball on the grass, the ball will stop; if you push a book across a table, the book stops moving. But this does not happen everywhere. In outer space, rockets and planets move and they do not slow down or stop. So something on Earth makes objects stop moving, and this is a force called friction. Every object that touches another object feels friction. Even when you throw something like a baseball, the baseball feels friction because of the air. This is called drag or air resistance. In outer space, there is no friction because outer space is a vacuum: there are no objects there, including no air.Gravity is another force that changes how objects move on Earth, but in outer space gravity is very small unless you are close to a planet or a star.

Newton's first law of motion also tells us that an object that is not moving will stay still unless something pushes or pulls it. This makes sense because a book on your bookshelf does not suddenly fly away.

Newton's second law

Newton's second law of motion says that bigger objects need a bigger force to change how they move, and smaller objects need a smaller force to change how they move. For example, it is easy to push a marble across the floor but it is really hard to push a car across the road. This is because the car is very heavy and the marble is not.

We sometimes write Newton's second law of motion as an equation: [math]\displaystyle{ F=ma }[/math]. [math]\displaystyle{ F }[/math] is the amount of force you need, [math]\displaystyle{ m }[/math] is the mass of the object you want to move, and [math]\displaystyle{ a }[/math] is the amount of acceleration (change of velocity) that the object gets when you try to move it. We can also write the equation as [math]\displaystyle{ F=\frac{dp}{dt} }[/math], where [math]\displaystyle{ p }[/math] is momentum and [math]\displaystyle{ \frac{dp}{dt} }[/math] is the way we write "change in momentum over time" using calculus. Momentum is the mass of an object times how fast it is moving (its speed): [math]\displaystyle{ p=m \times v }[/math], where [math]\displaystyle{ v }[/math] is the speed. A bumblebee has a small mass, but it moves very fast so it has lots of momentum. The Earth moves very slow, but it has a large mass so it also has lots of momentum.

Newton's third law

Newton's third law of motion says that forces always come in pairs. When you push a book, the book also pushes you, but it does not push you very far because you have a much larger mass. However, if you and your friend go ice skating and you push your friend, you and your friend both move back. Consider a book lying on a table. The weight of book is acting on the table in the downward direction. This is action. The reaction of table act on the book in upward direction.

A rocket works because of Newton's third law of motion: the bottom of the rocket makes very hot gas and the gas pushes the colder air. Then the rocket goes up because the colder air also pushes the bottom of the rocket. The force that makes a rocket go up is called thrust. Birds and airplanes fly because of Newton's third law of motion: this is because both birds and airplanes push air down when they move, and the air pushes them up. This force is called lift. Without lift, birds and airplanes fall on the ground.

Kinematic Equations

In physics, kinematics is the part of classical mechanics that explains the movement of objects without looking at what causes the movement or what the movement affects.

1-Dimensional Kinematics

1-Dimensional (1D) Kinematics are used only when an object moves in one direction: either side to side (left to right) or up and down. There are equations with can be used to solve problems that have movement in only 1 dimension or direction. These equations come from the definitions of velocity, acceleration and distance.

The first 1D kinematic equation deals with acceleration and velocity. If acceleration and velocity do not change. (Does not need include distance)
Equation: [math]\displaystyle{ V_f=v_i+at }[/math]
V_f is the final velocity.

v_i is the starting or initial velocity

a is the acceleration

t is time - how long the object was accelerated for.
The second 1D kinematic equation finds the distance moved, by using the average velocity and the time. (Does not need include acceleration)
Equation: [math]\displaystyle{ x=((V_f+V_i)/2)t }[/math]
x is the distance moved.

V_f is the final velocity.

v_i is the starting or initial velocity

t is time
The third 1D kinematic equation finds the distance travelled, while the object is accelerating. It deals with velocity, acceleration, time and distance. (Does not need include final velocity)
Equation: [math]\displaystyle{ X_f=x_i+v_it+(1/2)at^2 }[/math]
[math]\displaystyle{ X_f }[/math] is the final distance moved

x_i is the starting or initial distance

v_i is the starting or initial velocity

a is the acceleration

t is time
The fourth 1D kinematic equation finds the final velocity by using the initial velocity, acceleration and distance travelled. (Does not need include time)
Equation: [math]\displaystyle{ V_f^2=v_i^2+2ax }[/math]
V_f is the final velocity

v_i is the starting or initial velocity

a is the acceleration

x is the distance moved

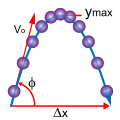
2-Dimensional Kinematics

2-Dimensional kinematics is used when motion happens in both the x-direction (left to right) and the y-direction (up and down). There are also equations for this type of kinematics. However, there are different equations for the x-direction and different equations for the y-direction. Galileo proved that the velocity in the x-direction does not change through the whole run. However, the y-direction is affected by the force of gravity, so the y-velocity does change during the run.

X-Direction Equations

Left and Right movement

The first x-direction equation is the only one that is needed to solve problems, because the velocity in the x-direction stays the same.
Equation: [math]\displaystyle{ X=V_x*t }[/math]
X is the distance moved in the x-direction

V_x is the velocity in the x-direction

t is time

Y-Direction Equations

Up and Down movement. Affected by gravity or other external acceleration

The first y-direction equation is almost the same as the first 1-Dimensional kinematic equation except it deals with the changing y-velocity. It deals with a freely falling body while its being affected by gravity. (Distance is not needed)
Equation: [math]\displaystyle{ V_fy=v_iy-gt }[/math]
V_fy is the final y-velocity

v_iy is the starting or initial y-velocity

g is the acceleration because of gravity which is 9.8 [math]\displaystyle{ m/s^2 }[/math] or 32 [math]\displaystyle{ ft/s^2 }[/math]

t is time
The second y-direction equation is used when the object is being affected by a separate acceleration, not by gravity. In this case, the y-component of the acceleration vector is needed. (Distance is not needed)
Equation: [math]\displaystyle{ V_fy=v_iy+a_yt }[/math]
V_fy is the final y-velocity

v_iy is the starting or initial y-velocity

a_y is the y-component of the acceleration vector

t is the time
The third y-direction equation finds the distance moved in the y-direction by using the average y-velocity and the time. (Does not need acceleration of gravity or external acceration)
Equation: [math]\displaystyle{ X_y=((V_fy+V_iy)/2)t }[/math]
X_y is the distance moved in the y-direction

V_fy is the final y-velocity

v_iy is the starting or initial y-velocity

t is the time
The fourth y-direction equation deals with the distance moved in the y-direction while being affected by gravity. (Does not need final y-velocity)
Equation: [math]\displaystyle{ X_fy=X_iy+v_iy-(1/2)gt^2 }[/math]
[math]\displaystyle{ X_fy }[/math] is the final distance moved in the y-direction

x_iy is the starting or initial distance in the y-direction

v_iy is the starting or initial velocity in the y-direction

g is the acceleration of gravity which is 9.8 [math]\displaystyle{ m/s^2 }[/math] or 32 [math]\displaystyle{ ft/s^2 }[/math]

t is time
The fifth y-direction equation deals with the distance moved in the y-direction while being affected by a different acceleration other than gravity. (Does not need final y-velocity)
Equation: [math]\displaystyle{ X_fy=X_iy+v_iy+(1/2)a_yt^2 }[/math]
[math]\displaystyle{ X_fy }[/math] is the final distance moved in the y-direction

x_iy is the starting or initial distance in the y-direction

v_iy is the starting or initial velocity in the y-direction

a_y is the y-component of the acceleration vector

t is time
The sixth y-direction equation finds the final y-velocity while it is being affected by gravity over a certain distance. (Does not need time)
Equation: [math]\displaystyle{ V_fy^2=V_iy^2-2gx_y }[/math]
V_fy is the final velocity in the y-direction

V_iy is the starting or initial velocity in the y-direction

g is the acceleration of gravity which is 9.8 [math]\displaystyle{ m/s^2 }[/math] or 32 [math]\displaystyle{ ft/s^2 }[/math]

x_y is the total distance moved in the y-direction
The seventh y-direction equation finds the final y-velocity while it is being affected by an acceleration other than gravity over a certain distance. (Does not need time)
Equation: [math]\displaystyle{ V_fy^2=V_iy^2+2a_yx_y }[/math]
V_fy is the final velocity in the y-direction

V_iy is the starting or initial velocity in the y-direction

a_y is the y-component of the acceleration vector

x_y is the total distance moved in the y-direction

Classical Mechanics Media

Diagram of orbital motion of a satellite around the Earth, showing perpendicular velocity and acceleration (force) vectors, represented through a classical interpretation.
The analysis of projectile motion is a part of classical mechanics.
Domain of validity for classical mechanics
Three stage Theory of impetus according to Albert of Saxony.
Sir Isaac Newton (1643–1727), an influential figure in the history of physics and whose three laws of motion form the basis of classical mechanics
Lagrange's contribution was realising Newton's ideas in the language of modern mathematics, now called Lagrangian mechanics.
Hamilton's greatest contribution is perhaps the reformulation of Lagrangian mechanics, now called Hamiltonian mechanics, forming the preferred choice by many prominent mathematical physics formulations.

Related pages

Other websites

Science aid: Newton's laws of motion
The Engineering Wiki's shorter page: Newton's laws of motion - engineers may improve it!
Newtonian Physics Archived 2011-04-25 at the Wayback Machine - an on-line textbook
Newtonian attraction for three Planets (Mathcad Application Server)
Gravity - Newton's Law for Kids
On Line Study Guide-study guide for high school students