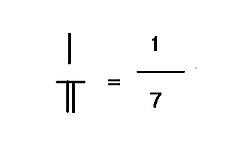Decimal
The decimal numeral system is the most usual way of writing numbers. It has ten as a starting point, or base. It is sometimes called the base ten or denary numeral system. The word "decimal" is also used to mean the dot (".") that is sometimes used to separate the positions of the numbers in this system. Indeed, the dot is the default decimal separator in English-speaking countries.[1][2]
Decimal notation
Decimal notation is the writing of numbers in the base-ten numeral system, which uses various symbols (called digits) for no more than ten distinct values (0, 1, 2, 3, 4, 5, 6, 7, 8 and 9[3]) to represent any numbers, no matter how large. These digits are often used with a decimal separator(such as "." or ","),[1][2] which indicates the start of a fractional part, and with one of the sign symbols + (positive) or − (negative) in front of the numerals to indicate sign.
There are only two truly positional decimal systems in ancient civilization: the Chinese counting rods system and Hindu-Arabic numeral system. Both required no more than ten symbols, while other numeral systems, such as Babylonian base-60 system, require more symbols.
Other rational numbers
Any rational number can be expressed as a unique decimal expansion. It may have to end with recurring decimals.
Ten is the product of the first and third prime numbers, is one greater than the square of the second prime number, and is one less than the fifth prime number. This leads to plenty of simple decimal fractions:
- 1/2 = 0.5
- 1/3 = 0.333333 ... (with 3 repeating forever, also called recurring)
- 1/4 = 0.25
- 1/5 = 0.2
- 1/6 = 0.166666 ... (with 6 recurring)
- 1/7 = 0.142857 ... (with 142857 recurring)
- 1/8 = 0.125
- 1/9 = 0.111111 ... (with 1 recurring)
- 1/10 = 0.1
- 1/11 = 0.090909 ... (with 09 recurring)
- 1.5/5.5 = 0.2727272722 ... (with 27 recurring)
- 1/12 = 0.083333 ... (with 3 recurring)
- 5.5/11 = 0.5
- 1/81 = 0.012345679012 ... (with 1234567890 recurring)
- 1/82 = 0.12195121951220 ... (with 12195 recurring)
History
Timeline of decimal usage
- c. 3500–2500 BC Elamites of Iran possibly used early forms of decimal system. [1][dead link] [2]
- c. 2900 BC Egyptian hieroglyphs show counting in powers of 10 (1 million + 400,000 goats, etc.) – see Ifrah, below
- c. 2600 BC Indus Valley Civilization, earliest known physical use of decimal fractions in ancient weight system: 1/20, 1/10, 1/5, 1/2. See Ancient Indus Valley weights and measures
- c. 1400 BC Chinese writers show familiarity with the concept: for example, 547 is written 'Five hundred plus four decades plus seven of days' in some manuscripts
- c. 1200 BC In ancient India, the Vedic text Yajur-Veda states the powers of 10, up to 1055
- c. 400 BC Pingala – develops the binary number system for Sanskrit prosody, with a clear mapping to the base-10 decimal system
- c. 250 BC Archimedes writes the Sand Reckoner, which takes decimal calculation up to 108 × 1016
- c. 100–200 The Satkhandagama written in India – earliest use of decimal logarithms
- c. 476–550 Aryabhata – uses an alphabetic cipher system for numbers that used zero (Sanskrit: शुन्य)
- c. 598–670 Brahmagupta – explains the Hindu-Arabic numeral system (modern number system) which uses decimal integers, negative integers, and zero
- c. 780–850 Muḥammad ibn Mūsā al-Ḵwārizmī – first to expound on algorism outside India
- c. 920–980 Abu'l Hasan Ahmad ibn Ibrahim Al-Uqlidisi – earliest known direct mathematical treatment of decimal fractions.
- c. 1300–1500 The Kerala School in South India – decimal floating point numbers
- 1548/49–1620 Simon Stevin – author of De Thiende ('the tenth')
- 1561–1613 Bartholemaeus Pitiscus – (possibly) decimal point notation
- 1550–1617 John Napier – use of decimal logarithms as a computational tool
- 1925 Louis Charles Karpinski – classic book The History of Arithmetic (Rand McNally & Company)
- 1959 Werner Buchholz – Fingers or Fists? (The Choice of Decimal or Binary representation) (Communications of the ACM, Vol. 2 #12, pp3–11)
- 1966 Isaac Asimov – Asimov on Numbers (ISBN 0-871-44246-5)
- 1974 Hermann Schmid – Decimal Computation (ISBN 0-471-76180-X)
- 2000 Georges Ifrah – The Universal History of Numbers: From Prehistory to the Invention of the Computer (ISBN 0-471-39340-1)
Natural languages
A straightforward decimal system, in which 11 is expressed as ten-one and 23 as two-ten-three, is found in Chinese languages except Wu, and in Vietnamese with a few irregularities. Japanese, Korean, and Thai have imported the Chinese decimal system. Many other languages with a decimal system have special words for teens and decades.
Incan languages such as Quechua and Aymara have an almost straightforward decimal system, in which 11 is expressed as ten with one and 23 as two-ten with three.
Some psychologists suggest irregularities of numerals in a language may hinder children's counting ability (Azar 1999).
Decimal Media
Diagram of the world's earliest known multiplication table (c. 305 BCE) from the Warring States period
The world's earliest decimal multiplication table was made from bamboo slips, dating from 305 BCE, during the Warring States period in China.
Related pages
References
- ↑ 1.0 1.1 "Compendium of Mathematical Symbols". Math Vault. 2020-03-01. Retrieved 2020-08-22.
- ↑ 2.0 2.1 Weisstein, Eric W. "Decimal Point". mathworld.wolfram.com. Retrieved 2020-08-22.
- ↑ Weisstein, Eric W. "Decimal". mathworld.wolfram.com. Retrieved 2020-08-22.
Bibliography ??
- Azar, Beth (1999), "English words may hinder math skills development", American Psychology Association Monitor, 30 (4).