Platonic solid
- The Platonic Solids
A Platonic solid is a kind of polyhedron (a three-dimensional shape). It has the following traits:
- Each of their faces is built from the same type of polygons.
- All the edges are the same, and all of them join two faces at the same angle.
- There are the same polygons meeting at every corner of the shape.
- The shape is convex, meaning the faces do not go through each other (intersecting), or span the same range (coplanar).
The Platonic solids
The following Platonic solids exist; there are only 5:
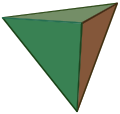
- Triangular pyramid, or Tetrahedron, has 4 sides, is made of triangles, and is the simplest kind of polyhedron.
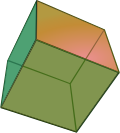
- Cube, or Hexahedron, has 6 sides, and is made of squares. It is a kind of prism.
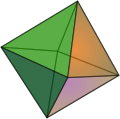
- Octahedron, has 8 sides, and is made of triangles. It is a kind of antiprism.
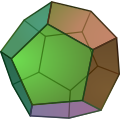
- Dodecahedron, has 12 sides, and is made of pentagons. It has the most vertices.
- Icosahedron, has 20 sides, and is made of triangles. It has the most faces.
Uses
There are a lot of uses for Platonic solids, but some of the main reasons are:the shapes are often used to make dice, because dice of these shapes can be made fair. 6-sided dice are very common, but the other numbers are commonly used in role-playing games. Such dice are commonly referred to as D followed by the number of faces (d8, d20 etc.).
The tetrahedron (4 sided), cube (6 sided), and octahedron (8 sided), are found naturally in crystal structures. The dodecahedron (12 sides) is combinatorially identical to the pyritohedron (in that both have twelve pentagonal faces), which is one of the possible crystal structures of pyrite. However, the pyritohedron is not a regular dodecahedron, but rather has the same symmetry as the cube.
In meteorology and climatology, global numerical models of atmospheric flow are of increasing interest which use grids that are based on an icosahedron (20 sides,refined by triangulation) instead of the more commonly used longitude/latitude grid. This has the advantage of better spatial resolution without singularities (i.e. the poles) at the expense of somewhat greater numerical difficulty.
Geometry of space frames is often based on Platonic solids.
Platonic Solid Media
Kepler's Platonic solid model of the Solar System from Mysterium Cosmographicum (1596)
Other websites
- Stella: Polyhedron Navigator Tool for exploring polyhedra
- Paper Models of Polyhedra Many links
- The Uniform Polyhedra
- Virtual Reality Polyhedra The Encyclopedia o Polyhedra
- London South Bank University Archived 2004-10-09 at the Wayback Machine Water structure and behavior
- Book XIII of Euclid's Elements.
- Interactive 3D Polyhedra Archived 2005-04-03 at the Wayback Machine in Java