Magnetic moment
| Electromagnetism |
|---|
 |
| Electricity · Magnetism · Magnetic permeability |
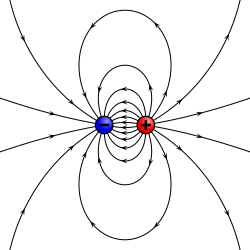
The magnetic moment of a magnet is a quantity that determines the force that the magnet can exert on electric currents and the torque that a magnetic field will exert on it. A loop of electric current, a bar magnet, an electron, a molecule, and a planet all have magnetic moments.
Both the magnetic moment and magnetic field may be considered to be vectors having a magnitude and direction. The direction of the magnetic moment points from the south to north pole of a magnet. The magnetic field produced by a magnet is proportional to its magnetic moment as well. More precisely, the term magnetic moment normally refers to a system's magnetic dipole moment, which produces the first term in the multipole expansion of a general magnetic field. The dipole component of an object's magnetic field is symmetric about the direction of its magnetic dipole moment, and decreases as the inverse cube of the distance from the object.
Two definitions of moment
In text books, two complementary approaches are used to define magnetic moments. In pre-1930's textbooks, they were defined using magnetic poles.[1] Most recent textbooks define it in terms of Ampèrian currents.
Magnetic pole definition
Physicists represent sources of magnetic moments in materials as poles. The North and South poles are an analogy to the positive and negative charges in electrostatics. Consider a bar magnet which has magnetic poles of equal magnitude but opposite polarity. Each pole is the source of magnetic force which weakens with distance. Since magnetic poles always come in pairs, their forces partially cancel each other because while one pole pulls, the other repels. This cancellation is greatest when the poles are close to each other i.e. when the bar magnet is short. The magnetic force produced by a bar magnet, at a given point in space, therefore depends on two factors: on both the strength [math]\displaystyle{ p }[/math] of its poles, and on the vector [math]\displaystyle{ \mathbf{l} }[/math] separating them. The moment is defined as[1]
- [math]\displaystyle{ \mathbf{m}=p\mathbf{l}. }[/math]
It points in the direction from South to North pole. The analogy with electric dipoles should not be taken too far because magnetic dipoles are associated with angular momentum (see Magnetic moment and angular momentum). Nevertheless, magnetic poles are very useful for magnetostatic calculations, particularly in applications to ferromagnets.[1] Practitioners using the magnetic pole approach generally represent the magnetic field by the irrotational field [math]\displaystyle{ \mathbf{H} }[/math], in analogy to the electric field [math]\displaystyle{ \mathbf{E} }[/math].
Current loop definition
Suppose a planar closed loop carries an electric current [math]\displaystyle{ I }[/math] and has vector area [math]\displaystyle{ \mathbf{S} }[/math] ([math]\displaystyle{ x }[/math], [math]\displaystyle{ y }[/math], and [math]\displaystyle{ z }[/math] coordinates of this vector are the areas of projections of the loop onto the [math]\displaystyle{ yz }[/math], [math]\displaystyle{ zx }[/math], and [math]\displaystyle{ xy }[/math] planes). Its magnetic moment [math]\displaystyle{ \mathbf{m} }[/math], vector, is defined as:
- [math]\displaystyle{ \mathbf{m}=I \mathbf{S}. }[/math]
By convention, the direction of the vector area is given by the right hand grip rule (curling the fingers of one's right hand in the direction of the current around the loop, when the palm of the hand is "touching" the loop's outer edge, and the straight thumb indicates the direction of the vector area and thus of the magnetic moment). [2]
If the loop is not planar, the moment is given as
- [math]\displaystyle{ \mathbf{m}=\frac{I}{2}\int\mathbf{r}\times{\rm d}\mathbf{r}. }[/math]
In the most general case of an arbitrary current distribution in space, the magnetic moment of such a distribution can be found from the following equation:
- [math]\displaystyle{ \mathbf{m}=\frac{1}{2}\int\mathbf{r}\times\mathbf{J}\,{\rm d}V, }[/math]
where [math]\displaystyle{ \mathbf{r} }[/math] is the position vector pointing from the origin to the location of the volume element, and [math]\displaystyle{ \mathbf{J} }[/math] is the current density vector at that location.
The above equation can be used for calculating a magnetic moment of any assembly of moving charges, such as a spinning charged solid, by substituting
- [math]\displaystyle{ \mathbf{J}=\rho \mathbf{v}, }[/math]
where [math]\displaystyle{ \rho }[/math] is the electric charge density at a given point and [math]\displaystyle{ \mathbf{v} }[/math] is the instantaneous linear velocity of that point.
For example, the magnetic moment produced by an electric charge moving along a circular path is
- [math]\displaystyle{ \mathbf{m}=\frac{1}{2}\, q\, \mathbf{r}\times\mathbf{v} }[/math],
where [math]\displaystyle{ \mathbf{r} }[/math] is the position of the charge [math]\displaystyle{ q }[/math] relative to the center of the circle and [math]\displaystyle{ \mathbf{v} }[/math] is the instantaneous velocity of the charge.
Practitioners using the current loop model generally represent the magnetic field by the solenoidal field [math]\displaystyle{ \mathbf{B} }[/math], analogous to the electrostatic field [math]\displaystyle{ \mathbf{D} }[/math].
Magnetic moment of a solenoid
A generalization of the above current loop is a multi-turn coil, or solenoid. Its moment is the vector sum of the moments of individual turns. If the solenoid has [math]\displaystyle{ N }[/math] identical turns (single-layer winding),
- [math]\displaystyle{ \mathbf{m}=N I \mathbf{S}. }[/math]
Units
The unit for magnetic moment is not a base unit in the International System of Units (SI) and it can be represented in more than one way. For example, in the current loop definition, the area is measured in square meters and [math]\displaystyle{ I }[/math] is measured in amperes, so the magnetic moment is measured in ampere–square meters ([math]\displaystyle{ \text{A m}^2 }[/math]). In the equation for torque on a moment, the torque is measured in Newton.meters and the magnetic field in tesla, so the moment is measured in N.m per Tesla ([math]\displaystyle{ \text{N.m T}^{-1} }[/math]). These two representations are equivalent:
- [math]\displaystyle{ \,\text{A m}^2 = \,\text{N.m T}^{-1}. }[/math]
In the CGS system, there are several different sets of electromagnetism units, of which the main ones are ESU, Gaussian, and EMU. Among these, there are two alternative (non-equivalent) units of magnetic dipole moment in CGS:
and (more frequently used)
The ratio of these two non-equivalent CGS units (EMU/ESU) is equal exactly to the speed of light in free space, expressed in cm/s.
All formulas in this article are correct in SI units, but in other unit systems, the formulas may need to be changed. For example, in SI units, a loop of current with current I and area A has magnetic moment I×A (see below), but in Gaussian units the magnetic moment is I×A/c.
| Particle | Magnetic dipole moment in SI units (10−27 J/T) | Spin quantum number (dimensionless) |
|---|---|---|
| electron | -9284.764 | 1/2 |
| proton | 14.106067 | 1/2 |
| neutron | -9.66236 | 1/2 |
| muon | -44.904478 | 1/2 |
| deuteron | 4.3307346 | 1 |
| triton | 15.046094 | 1/2 |
For relation between the notions of magnetic moment and magnetization see magnetization.
References and notes
- ↑ 1.0 1.1 1.2 Brown, Jr., William Fuller. Magnetostatic Principles in Ferromagnetism. North-Holland.
- ↑ Feynman, Richard P.; Leighton, Robert B.; Sands, Matthew (2006). The Feynman Lectures on Physics. Vol. 2. ISBN 0-8053-9045-6.
- ↑ See NIST's Fundamental Physical Constants website http://physics.nist.gov/cgi-bin/cuu/Results?search_for=+magnetic+moment